Vignetting을 이용한 광축 정렬 측정 알고리즘(1)
안녕하세요 엄성민입니다.
이래 저래 찾아보아도 답이 잘 없네요,,
3차원 공간상에 반지름 r인 원형 물체가 있습니다.
이것을 2차원 스크린에 투영시킵니다.
면상체의 빛 --> 원 --> 스크린
이때 스크린과 원의 중심을 잇는 수직선에 대해 원이 수평 방향으로 x_theta 만큼 각이 틀어져 있다면,
투영되는 타원 방정식은
{x^2 / [(r*|cos(x_theta)|]^2} + {y^2 / r^2} = 1
의 형태가 될 것입니다.
(원점은 원은 중심과 스크린을 잇는 수직선이 스크린과 만나는 점이며, x 축은 스크린의 가로축이며, y축은 스크린의 세로방향축)
이 상태에서 스크린과 원의 중심을 잇는 수직선에 대해 원이 수직 방향으로도 y_theta 만큼 틀어진다면 투영되는 타원 방정식은 어떻게 되어야 할까요?
즉, 투영되는 타원을 theta_x, theta_y로 표현해야 합니다.
[2012-09-13] 네이버 지식인에 위 질문에 대한 다음과 같은 답글이 달렸습니다.
To answer your question, we need to track what happens to the normal vector of the circle.
Let's call x-axis pointing to the right, y-axis going up, and z-axis coming out of the screen.
"이 상태에서 스크린과 원의 중심을 잇는 수직선에 대해 원이 수직 방향으로도 y_theta 만큼 틀어진다면"
sounds like a lab-axis rotation. (You could have been more precise in describing the second rotation by saying whether it is body-axis rotation, or lab-axis rotation.)
At first rotation, the body frame and the lab frame are aligned and there is no ambiguity. It is rotation about the x-axis in both frames. But after the first rotation, two frames are no longer aligned and the second rotation about "y-axis" becomes ambiguous. The lab frame y-axis is still pointing straight up as before but the body Y-axis is now tilted a little bit into the screen. I assume you meant the lab-axis rotation.
The Normal Vector of the original Circle: n0 = (0, 0, 1)
The First Rotation about x-axis:
The Second Rotation about the Lab Frame y-axis: (what you described)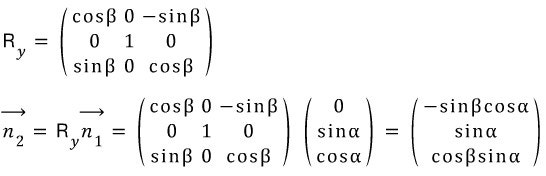
The projection of the normal vector on to the screen becomes the direction of the minor axis of the ellipse. So the major axis makes the angle θ with the x-axis on the screen.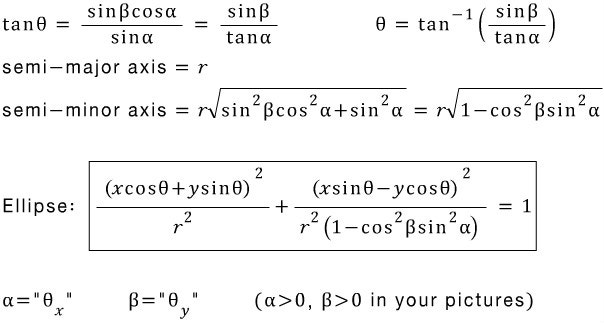
Based on the rotated ellipse equation:
By the way, in case of the second rotation were about the Body Frame Y-axis: (not what you described)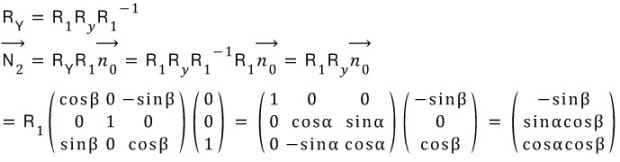
[2012-09-13] 네이버 지식인의 답변자께서 오류일부를 수정하였습니다.
To answer your question, we need to track what happens to the normal vector of the circle.
Let's call x-axis pointing to the right, y-axis going up, and z-axis coming out of the screen.
"이 상태에서 스크린과 원의 중심을 잇는 수직선에 대해 원이 수직 방향으로도 y_theta 만큼 틀어진다면"
sounds like a lab-axis rotation. (You could have been more precise in describing the second rotation by saying whether it is body-axis rotation, or lab-axis rotation.)
At first rotation, the body frame and the lab frame are aligned and there is no ambiguity. It is rotation about the x-axis in both frames. But after the first rotation, two frames are no longer aligned and the second rotation about "y-axis" becomes ambiguous. The lab frame y-axis is still pointing straight up as before but the body Y-axis is now tilted a little bit into the screen. I assume you meant the lab-axis rotation.
The Normal Vector of the original Circle: n0 = (0, 0, 1)
The First Rotation about x-axis:
The Second Rotation about the Lab Frame y-axis: (what you described)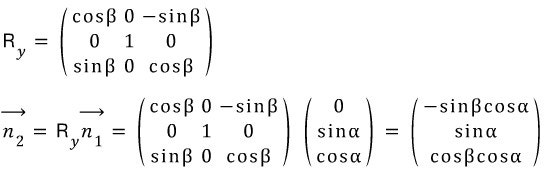
The projection of the normal vector on to the screen becomes the direction of the minor axis of the ellipse. So the major axis makes the angle θ with the x-axis on the screen.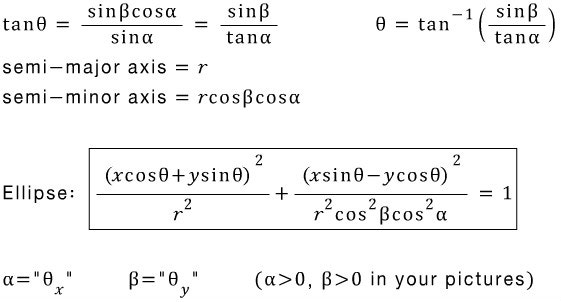
Based on the rotated ellipse equation:
By the way, in case of the second rotation were about the Body Frame Y-axis: (not what you described)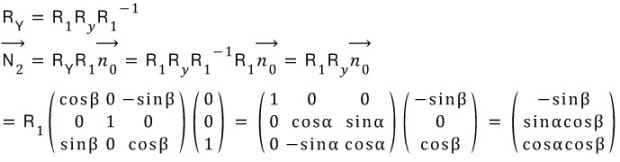
아울러 의견 내용도 첨부합니다.
yskimmat2012-09-13 16:47:04
알파와 베타의 회전에는 active view를 적용해서 실제로 물체를 돌리는 관점이고 좌표계는 그대로 입니다.
마지막에 장축의 방향과 그 공식을 찾는 과정은 좌표계변환 (passive view = coordinate transform)을 적용했습니다.
yskimmat2012-09-13 16:37:13
단축 r*cosB*cosA
회전 매트릭스는
| cos& +/-sin& |
|-/+sin& cos& |
저도 몇가지 실수를 했었지만 지금 답이 맞습니다
회전각의 +/- 방향에 대해서 말씁드리면 사진은 x축괴 y축에 대해 각각 음각으로 돌리고 있습니다. (right hand 룰 로 양각을 정의 한다고 할때) 그래서 제가 메이트릭스를 양수인 알파와 베타를 써서 사진과 같이 되게 한겁니다.
그러니까 "x_theta" 라고 말씀하신게 right hand 룰의 각이면
알파 = - "x_theta"
베타 = - "y_theta" 가 됩니다.
그리고 많은 사람들이 회전 행렬 "공식"만 외워서 적용하는 경우에 부호가 틀리는 일이 많은데 그 이유중에 하나가 회전 (active view)과 회전 좌표변환 (passive view)은 서로 역행렬이 되니까 같은 걸 두고도 서로 달리 표현하는 경우가 생기기 때문입니다. (제가 직업상 이분야에서 일했었습니다.)
하지만 문제가 정사영이기 때문에 양각으로 돌리던 음각으로 돌리던 단축의 길이가 cos알파cos베타 가 되는 건 변함이 없습니다. 다만 단축의 방향은 차이가 납니다.

질문 작성자2012-09-13 15:58:36
감사합니다 yskimmat 님,
1. 중간에 표현된 투사 타원에 대한 방정식에 있어, 장축 r, 단축 r*cosB*sinA
로 이해 됩니다. 다만 평면상의 회전에 있어, 위 수식에 의하면
회전 매트릭스는
| cos& sin& |
| sin& -cos& |
로 보여지는데, 이것은 시계방향 또는 반시계 방향 회전에 대한 매트릭스가 아닌 것 같습니다. 오류가 있는 것인지 제가 잘못 이해하고 있는 것인지 확인하고 싶습니다.
최종 목적은 장축, 단축, 회전각을 알고 있는 타원으로 부터 투사된 원형과의 틀어진 각도 alpha, beta의 절대값을 알아내는데 있습니다.
2. 맨아래의 타원 회전에 대한 base에서 표현된 회전 행렬은 시계방향의 theta에 대한 것이 아닌지, 이것과 그림이 상반되지 않는지 확인 바랍니다.
친절한 답변에도 불구하고 요청사항이 발생하여 죄송합니다




